問16
MTBFがx時間, MTTRがy時間のシステムがある。使用条件が変わったので,MTBF,MTTRがともに従来の1.5倍になった。新しい使用条件での稼働率はどうなるか。
【稼働率の公式】
MTBFを$ x $、MTTRを$ y $とした時 $ \frac{x}{ ( x + y ) } $
稼働率の公式を知っていれば解くことが出来ます。
今回は $ x , y $ とも従来の1.5倍となっているので下記の式になるはずです。
$ \displaystyle \frac{1.5x}{ 1.5x + 1.5y } $
次に分母について、1.5でくくることが出来ますね。
$ \displaystyle \frac{1.5x}{ 1.5( x + y ) } $
これを約分すると…
$ \displaystyle \frac{x}{ x + y } $ となり、従来の稼働率と同じであることが分かります。
よって答えは【イ】となります。
問18
Javaなどのバイトコードプログラムをインタプリタで実行する方法と,コンパイルしてから実行する方法を,次の条件で比較するとき,およそ何行以上のバイトコードであれば,コンパイル方式の方がインタプリ夕方式よりも処理時間(コンパイル時間も含む)が短くなるか。
〔条件〕
①実行時間はプログラムの行数に比例する。
②同じ100行のバイトコードのプログラムをインタプリタで実行すると0.2秒掛かり,コンパイルしてから実行すると0.003秒掛かる。
③コンパイル時間は100行当たり0.1秒掛かる。
④コンパイル方式の場合は,プログラムの行数に関係なくファイル入出力,コンパイラ起動などのために常に0.15秒のオーバヘッドが掛かる。
⑤プログラムファイルのダウンロード時間など,そのほかの時間は無視して考える。
まず条件をインタプリタ方式とコンパイル方式に分けましょう。
〔インタプリ夕方式〕
①100行のコード実行時間は0.2秒
〔コンパイル方式〕
①プログラムの時間に100行当たり0.003秒かかる。
②コンパイル時間は100行当たり0.1秒かかる。
③行数に関係なく、0.15秒かかる。
インタプリ夕方式は下記の等式が成り立ちます。
コード100行を $ l $ すると
$ l \times 0.2 = 0.2l $
コンパイル方式も同様に考えましょう。
コード100行を $ l $ すると
①で成り立つ式は $ 0.003 \times l = 0.003l $
②で成り立つ式は $ 0.1 \times l = 0.1l $
③はそのまま$ 0.15 $だから全て合わせて
$ 0.1l + 0.003l + 0.15 = 0.103l +0.15 $
となります。
今回はコンパイル方式の処理時間がインタプリ夕方式よりも短くなれば良いです。
しかし、わかりにくいのでコンパイル方式とインタプリ夕方式の処理時間分岐点を求めて上げましょう。
両方の処理時間が一緒になると仮定すれば
$ 0.2l = 0.103l + 0.15 $ となります。
後はこの等式を解けば
$ 0.2l – 0.103l = 0.15 $
$ 0.097l = 0.15 $
$ l = 1.54639… $
となります。
$ l $はコード100行と定義したので100倍しましょう。
$ l \fallingdotseq 154 $
ここから、154行まではインタプリタ方式がよく、155行からはコンパイル方式の方が良くなると分かりました。
よって答えは【エ】となります。
問20
アノードコモン型7セグメントLEDの点灯回路で,出力ポートに16進数で92を出力したときの表示状態はどれか。ここで,P7を最上位ビット(MSB),P0を最下位ビット(LSB)とし,ポート出力が0のとき,LEDは点灯する。
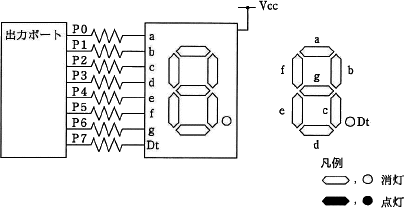
基数変換が出来るかどうかの問題です。
16進数は4ビット毎に2進数表記出来ましたね。戻しましょう。
$ 92_{(16)} = 1001 0010 $となります。
少し引っかかるポイントとして、出力が「0」の時に点灯するとされています。
P7が最上位ビットでP0が最下位ビットなので
P7 = 1 , P6 = 0 ‥・・ P0 = 0 となります。
後はそれぞれどこに「0」が来るか考えましょう。
図から「 $ a , c , d , f , g $」に0が来ますので、このような図になり、答えは【ウ】となります。
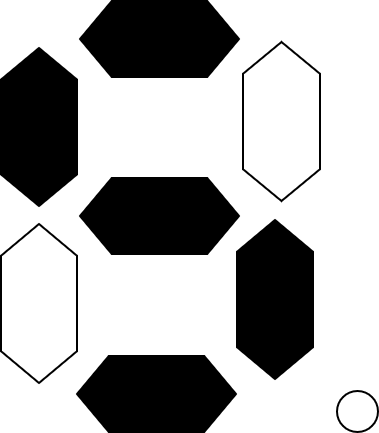
問21
リトルエンディアン方式のメモリは位置です。
リトルエンディアン…?となりましたので調べました。
リトルエンディアン
最下位ビットを最下位アドレスから配置する方式です。
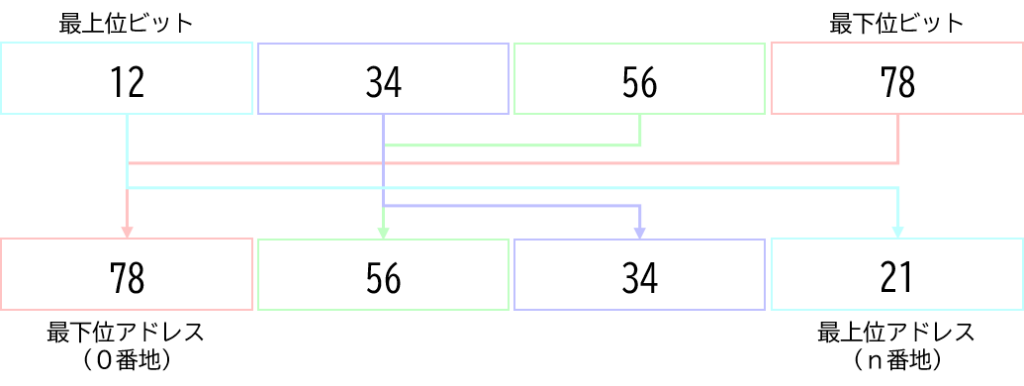
これの特徴は与えられたビットと格納される順番は反対になる所です。
ビックエンディアン
最上位ビットは最下位アドレスから配置する方式です。
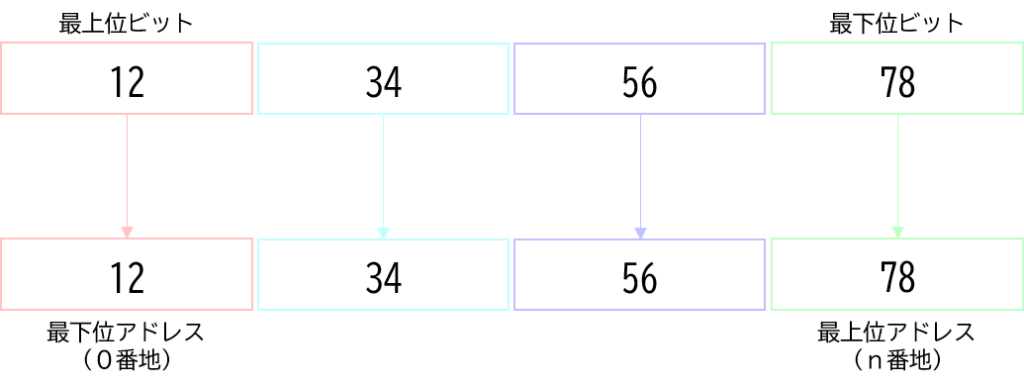
これの特徴は与えられたビットと格納される順番が同じになる所です。
今回はリトルエンディアン方式ですので、与えられたデータ「ABCD1234」を逆にすれば良いですね。
「 43|21|DC|BA 」となり答えは【イ】となります。
問22
真理値表に示す3入力多数決回路はどれか。
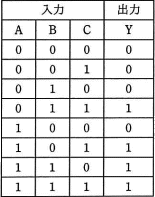
まずはやっぱりグループ分けをしましょう。前回も論理回路は必ず、両方が「0」、片方が「1」、両方が「1」の時の演算結果は必ず同じになりますと解説しました。
今回も次の4パターンが考えられます。
①全て「0」=0
②1つ「1」=0
③2つ「1」=1
④全て「1」=1
となると分かります。つまり、実際に検証すれば良いのは4パターンであるということです。
後は注意して検証していきましょう。
問23
顧客に,英大文字A~Zの26種類を用いた顧客コードを割り当てたい。現在の顧客総数は8,000人であって,新規顧客が毎年2割ずつ増えていくものとする。3年後まで顧客全員にコードを割り当てられるようにするための,顧客コードの最も少ない桁数は幾つか。
①3年後の顧客数を求めましょう。毎年2割ずつ増えていきますから、
1年目:$ 8000 \times 1.2 = 9600 $
2年目:$ 9600 \times 1.2 = 11520 $
3年目:$ 11520 \times 1.2 = 13824 $
最終的な顧客数は13824人になると分かりました。
②表せるコード数を求めましょう。
26種類のアルファベットを1桁使った時は、勿論A~Zまでの26種類を表すことが出来ますね。
それでは2桁使った時はどうでしょうか。例えばAA,AB,AC,AD, ・・・ ,ZX,ZY,ZZ と言ったようにAにはA~Zの26種類を作ることが出来ます。他のアルファベットも同じなので、$ 26 \times 26 $で $ 26^2 $であることが分かります。
これを一般化すると
文字種類$ k $の $ n $桁の表現可能数は $ k^n $
と分かります。
後はこれに当てはめれば良いので
1桁=$26$種類
2桁=$26^2 = 676 $種類
3桁=$ 26 ^ 3 = 26^2 \times 26 = 676 \times 26 = 17576 $
で $ 13824 \lt 17576 $ となって、全ての顧客をコードで表現できるようになりました。
よって答えは3桁の【ア】となります。
問26
次のような繰返し構造をもったデータを,第3正規形に正規化したものはどれか。ここで,下線部分は主キーを表す。また,単位と単価は商品コードごとに決まるものとする。

【正規化(ざっくり)】
第1正規形・・・繰り返しをなくす
第2正規形・・・主キーで分離する。
第3正規形・・・主キー以外で分離する。
今回は第3正規形まで行えと書いてありますので順番にやっていきましょう。
第1正規形は省略します。
第2正規形は主キーで分離していきます。
主キーは一見「伝票番号」だけに見えますが、繰り返しをなくした時、1つの伝票番号だけでは複数個購入されていると一意に決定出来ません。
なので商品コードも主キーとして複合キーにしてあげなければなりません。
これ毎に分離していくと
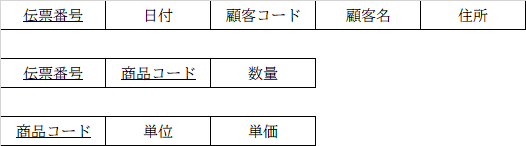
このようになります。
1行目は伝票番号が分かれば日付・顧客コード・顧客名・住所の4つが分かります。数量や商品コードは伝票番号だけでは一意に決まらないので不適切です。
2行目は伝票番号と商品コードで数量が特定できますので分離する必要があります。
3行目は商品コードが分かればその商品の単位と単価が一意に分かるので分離する必要があります。
最後に第3正規形にしましょう。顧客コードで分離できそうですね。
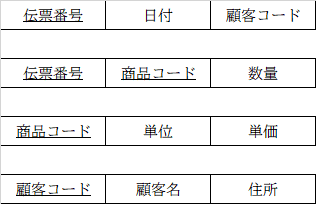
伝票番号で顧客は特定したいので「顧客コード」は残してあげてください。
問30
100Mビット/秒のLANを使用し,1件のレコード長が1,000バイトの電文を1,000件連続して伝送するとき,伝送時間は何秒か。ここで,LANの伝送効率は50%とする。
単位変換に注意しましょう。
まず送信しなければならないデータ量を求めてあげましょう。
$ 1000B \times 1000 = 1,000,000B $ となります。
転送速度はビットですので単位を変えてあげましょう。
$ 1,000,000B \times 8b = 8,000,000bit $
転送速度は「Mbit」ですので送信データ量も「Mbit」に変えてあげましょう。
$ 8,000,000 \div 1,000,000 = 8Mbit $
伝送効率が50%であるので50Mbit/秒で送ることが出来ます。
後はここから秒数を求めれば終わりなので
$ 8Mbit \div 50Mbit/s = 0.16s $ となり答えは【ウ】となります。

