問1
次の10進小数のうち、2進数で表すと無限小数になるものはどれか。
小数点にも「重み」がある! (0.5 -> 0.25 -> 0.125 ・・・)
無限小数になるということはすなわち有限小数にならないとも言い換えることが出来ます。
有限小数は10進小数が2進数で表せれば良いです。
つまり、1つ以上の重みでその10進小数を表すことが出来れば有限小数であると言えますね。
【ア】はどの重みでも構成されませんので無限小数です。
【イ】は上のポイントで3つ目の重みで構成出来るので有限小数です。
【ウ】は上のポイントで2つ目と3つ目の重みで構成出来るので有限小数です。
【エ】は上のポイントで1つ目の重みで構成出来るので有限小数です。
問3
2桁の2進数 $ x_{1}x_{2} $ が表す整数を $ x $とする。2進数 $ x_{2}x_{1} $が表す整数を、$ x $の式で表したものはどれか。ここで、int($ r $)は非負の実数$ r $の小数点以下を切り捨てた整数を表す。
まず2桁の2進数で表すことが出来る整数を考えましょう。
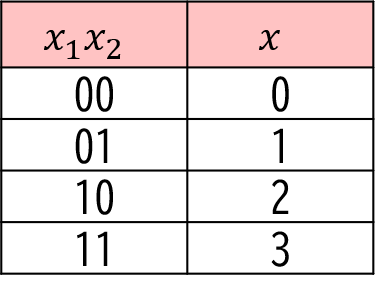
次に$ x_{1}x_{2} $を入れ替えましょう。その時の整数(ここでは $ x’ $とします )も考えましょう。
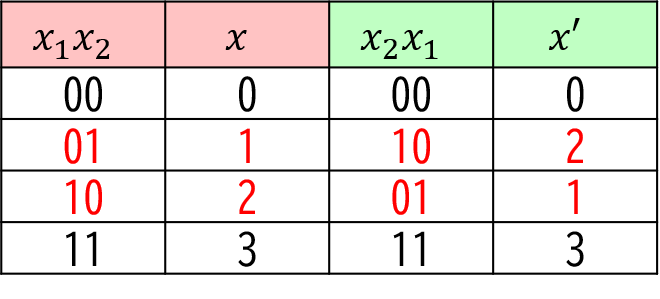
このとき、整数$x$と整数$x’$の値に着目して、値が変わっているものについて、これを式に代入すれば良いです。
ア・イは2進数 $10$を代入した時点で値が3を超えるため、この時点で検証する必要性が有りません。
よって検証すべきなのは残りの選択肢ウ・エの二つであると分かります。
①2進数「10」= $ x = 2 $ の時
選択肢【ウ】
$ 2 \times 2 – 3 int(\frac{2}{2}) $
$ = 4 – 3 \times 1 $
$ = 1 $
選択肢【エ】
$ 2 \times 2 – 4 int(\frac{2}{2}) $
$ = 4 – 4 \times 1 $
$ = 0 $
答えとして出るのは$ x’ $であって欲しいので、この時点で選択肢【ウ】しか有りません。
問6
入力記号,出力記号の集合が{0,1}であり,状態遷移図で示されるオートマトンがある。0011001110 を入力記号とした場合の出力記号はどれか。ここで,S1は初期状態を表し,グラフの辺のラベルは,入力/出力を表している。
〔状態遷移図〕
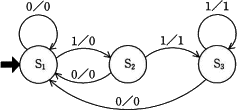
この問題はそのまま指示されたことを行えば良い問題です。
初期状態は $ S_{1} $と指示されているので、そこからスタートします。
それぞれの指示について解説します。
【 $ S_{1} $ の指示 】
入力が0の時 → 出力は1
入力が1の時 → 出力は0・$ S_{2} $ へ
【 $ S_{2} $ の指示 】
入力が0の時 → 出力は0・$ S_{1} $ へ
入力が1の時 → 出力は1・$ S_{3} $ へ
【 $ S_{3} $ の指示 】
入力が0の時 → 出力は0・$ S_{1} $ へ
入力が1の時 → 出力は1
【出力結果】

問7
A,B,C,Dの順に到着するデータに対して、一つのスタックだけを用いて出力可能なデータ列はどれか。
【スタック・キュー】
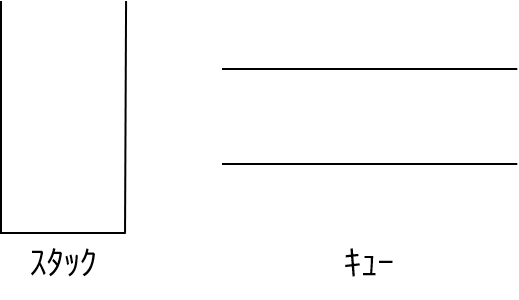
スタック・キューが出てきたら図を書きましょう。スタックは最初に入れたデータが最後に出てくる
FILO方式のデータ操作です。
【ア】:不適切
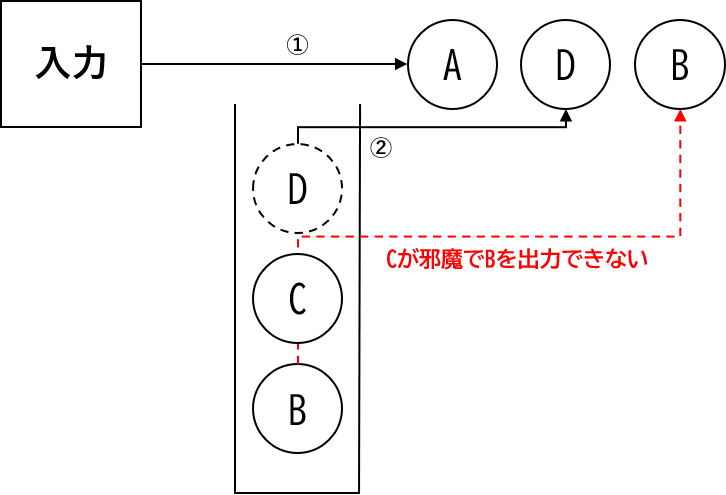
【イ】:不適切
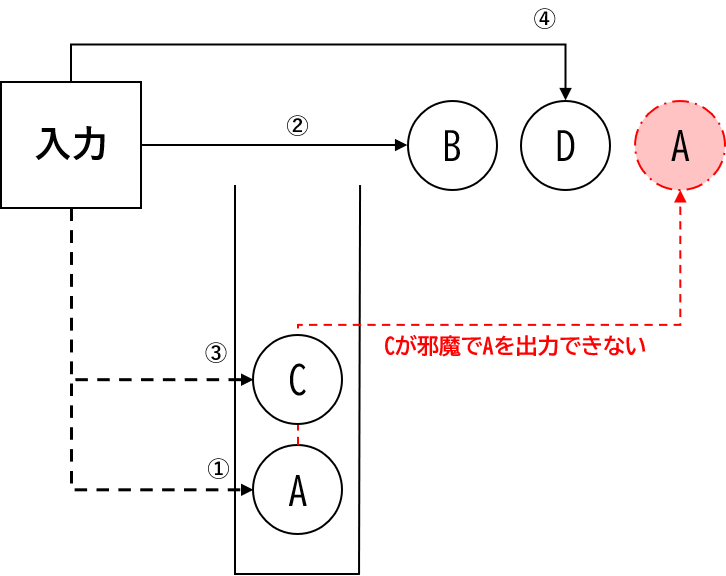
【ウ】:正解
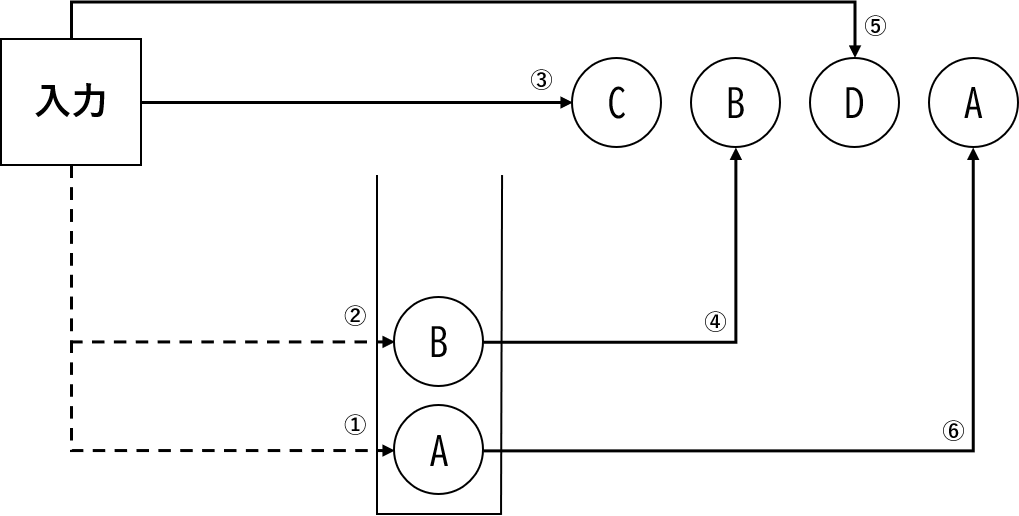
問8
双方向のポインタをもつリスト構造のデータを表に示す。この表において新たな社員Gを社員Aと社員Kの間に追加する。追加後の表のポインタa~fの中で追加前と比べて値が変わるポインタだけをすべて列記したものはどれか。
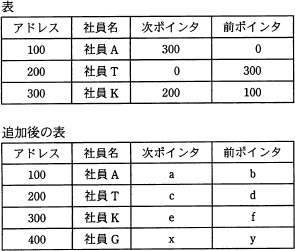
変化するポインタを見つける問題です。双方向のポインタがあるので、変わると考えられるのは
X → 新データ → Y であれば、Xの次ポインタとYの前ポインタの二つであると分かります。
よって答えは、Aの次ポインタである $ a $とKの前ポインタである$ f $の【ウ】となります。
問9
キーが小文字のアルファベット1文字(a, b, …, z のいずれか)であるデータを,大きさが10のハッシュ表に格納する。ハッシュ関数として,アルファベットのASCIIコードを10進表記法で表したときの1の位の数を用いることにする。衝突が起こるキーの組合せはどれか。ASCIIコードでは,昇順に連続した2進数が,アルファベット順にコードとして割り当てられている。
問題文通りに図を作成しましょう。問題文には、
① ハッシュ関数は10進表記法で表した時の1の位
② 昇順に連続した2進数である
③ アルファベット順である
以上を考慮すれば、それぞれのアルファベットに対して連番の10進数を付ければ良いことが分かります。

後は選択肢の組み合わせを検討すれば終わりです。
【ア】$a$と$i$は1・9で条件に合わず不適。
【イ】$b$と$r$は2・18で条件に合わず不適。
【ウ】$c$と$l$は3・12で条件に合わず不適。
【エ】$d$と$x$は4・24で1の位が同じという条件を満たすので適切。
問10
正の整数Mに対して,次の二つの流れ図に示すアルゴリズムを実行したとき,結果xの値が等しくなるようにしたい。a に入れる条件として,適切なものはどれか。
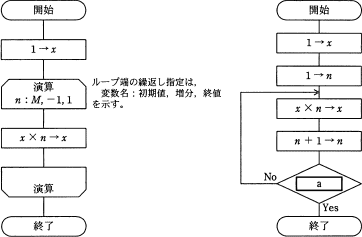
トレースしても良いですが、今回は論理的に考えましょう。
しかし、整数Mを与えなければわかりにくいのでそれは適当に設定しましょう。
今回は $ M = 10 $ とします。
演算ループの処理は増分が「-1」で、終値が「1」であるので $ M = 1 $になるまで行われることが分かります。(中ループは9回)
隣の流れ図に移りましょう。$ a $の条件に適合した時に終了処理を行えば良いと書いてあり、増分の役割をする変数は $ n $です。
普通であれば $ n \geq M $ で良いのですが、今回は no がループの条件となっているので、これを否定してあげましょう。
否定すれば $ n > M $ になり、選択肢【ウ】が適切であると分かります。

