問52【エ】
図のアローダイアグラムにおいて,プロジェクト全体の期間を短縮するために,作業A~Eの幾つかを1日ずつ短縮する。プロジェクト全体を2日短縮できる作業の組合せはどれか。
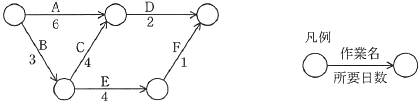
まずはプロジェクト全体の作業日数を求めなければなりません。
プロジェクト全体の作業日数はクリティカルパスで表されます。
クリティカルパス・・・開始点から終了点までで所要日数が最も多くなるルート
よって、クリティカルパスは、B→C→D=9日であると分かりました。
今回行いたい処理は、プロジェクト全体を2日短縮しなければなりません。
つまり、クリティカルパスから2日間引いた7日にしたい訳です。
この時点で、クリティカルパスの2つを短縮しないといけないのは分かるかと思います。(この時点で、ア・イの選択肢はあり得ない)
なので残りの【ウ】と【エ】を検証しましょう。
【選択肢:ウ(B,C,E)】
A→Dは8日となって不適切です。
【選択肢:エ(B,D)】
いずれのパターンも7日となるため適切。よって解答は【エ】となる。
問53【ウ】
10人が0.5kステップ/人日の生産性で作業するとき,30日間を要するプログラミング作業がある。10日目が終了した時点で作業が終了したステップ数は,10人の合計で30kステップであった。予定の30日間でプログラミングを完了するためには,少なくとも何名の要員を追加すればよいか。ここで,追加する要員の生産性は,現在の要員と同じとする。
最初の1行でこのプログラミング作業の総ステップ数を求めましょう。
計算式ⅰ:$ 10 \times 0.5 \times 30 = 150k $
10日時点で30kステップ終了しているから、残りの必要ステップ数は
計算式ⅱ:$ 150k – 30k = 120k $
現在のまま行えば20日後のステップ数は60kであり、あと60kステップ足りない。
つまり10人を追加した20人体制で行えば、予定通り完了することが出来る。
よって【ウ】が正解である。
問54【エ】
プロジェクトメンバが16人のとき,2人ずつの総当たりでプロジェクトメンバ相互の顔合わせ会を行うためには,延べ何時間の顔合わせ会が必要か。ここで,顔合わせ会1回の所要時間は0.5時間とする。
まず16人が2人ずつの総当たりというのは、異なるn個からr個選ぶ組み合わせと同じであるとわかる。
$ {}_{ 16 } C _{2}= \frac{16 \times 15}{2 \times 1} $となり、答えは120となる。
しかし、1回当たりの所要時間は0.5時間であるから
$ 120 \times 0.5 = 60 $で、よって60の【エ】が正答となる。
問63【イ】
改善の効果を定量的に評価するとき,複数の項目で評価した結果を統合し,定量化する方法として重み付け総合評価法がある。表の中で優先すべき改善案はどれか。
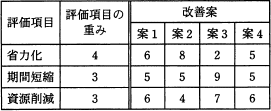
それぞれの重みで案1から案4を乗じれば良い。
案1: $ 24 + 15 +18 = 57 $
案2: $ 32 + 15 +12 = 59 $
案3: $ 8 + 27 + 21 = 56 $
案4: $ 20 + 15 + 18 = 53 $
一番高い値は案2であるから、答えは【イ】となる。
問72【エ】
ある工場では表に示す3製品を製造している。実現可能な最大利益は何円か。ここで,各製品の月間需要量には上限があり,また,組立て工程に使える工場の時間は月間200時間までで、複数種類の製品を同時に並行して組み立てることはできないものとする。
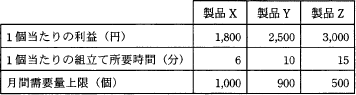
まずそれぞれの1分当たりの利益額を求めましょう。
製品X= $ 1800 \div 6 = 300 $
製品Y= $ 2500 \div 10 = 250 $
製品Z= $ 3000 \div 15 = 200 $
上記より、製品X→製品Y→製品Zの順番で生産するのが良いことが分かる。
組み立て工程に利用出来る工場の時間は月間200時間であるから、分に直すと、
$ 200 \times 60 = 12000m $である。
ここから、製品Xを全て作成することによって使用される時間と得る利益は次の通りである。
【製品X】
時間: $ 6 \times 1000 = 6000m $(所要時間×月間需要量)
残り時間: $ 12000 – 6000 = 6000m $
利益: $ 1800 \times 1000 = 1,800,000 $ (生産量×利益)
次に製品Yを生産しようとするが、月間需要量上限数分生産すると、9000分を要するため生産出来ない。よって、生産量を始めに計算する。
【製品Y】
生産量: $ 6000 \div 10 = 600 $(残り時間÷所要時間)
利益:$ 2500 \times 600 = 1,500,000 $
※残り時間や時間は、時間を製品Yの時点で全て使い切るため、求める必要は無い。
最後に製品Xと製品Yの利益額をそれぞれ足し合えば、
$ 1,800,000 + 1,500,000 = 3,300,000 $となり、答えは【エ】となる。
問73【ウ】
図は,製品Aの構成部品を示している。この製品Aを10個生産する場合,部品Cの手配数量は何個になるか。ここで,括弧内の数字は上位部品1個当たりの所要数量であり,部品Cの在庫は5個とする。
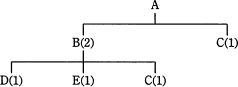
この図は、Aを作るのにBが2つ、Cが1つ必要であることを示しています。
そして、Bを作るのにD・E・Cがそれぞれ1つずつ必要であることも示しています。
ここで、Bを2個作るのにと解釈すると間違える原因となります。
あとはAを10個作る時にBは20個、Cは10個必要です。
Bの部品としてCは更に20個必要です。
この2つを合計して30個がCの必要数です。
問題文より部品Cの在庫は5個あるので、
$ 30 – 5 = 25 $で答えは25の【ウ】となる。

