問31【ウ】
本社と工場との間を専用線で接続してデータを伝送するシステムがある。このシステムでは2,000バイト/件の伝票データを2件ずつまとめ,それに400バイトのヘッダ情報を付加して送っている。伝票データは,1時間に平均100,000件発生している。回線速度を1Mビット/秒としたとき,回線利用率はおよそ何%か。
まず1回の送信データ量を求めましょう。
伝票データは1件2000Bです。これが2件あり、更にこれに400Bを付加して送信しています。
つまり、 $2000B \times 2 + 400 = 4400B$が1回当たりの送信データ量であることが分かります。
伝票データは1時間に平均100,000件発生しています。(送信が100,000回ではありません)
伝票データは2件ずつ送られるので、50,000回送信すれば良いと分かります。
よって、転送データ量は
$ 4400B \times 50000 = 220,000,000B = 220MB $となります。
後は1時間で送れる最大転送可能量を求め、その割合を求めれば解が出ます。
1秒間に1Mbit送れるということは、
$ 1000Kb \div 8 = 125KB $ となり、1秒間に125KB送れると分かります。
(小数点は間違える原因となるので工夫しましょう)
後はこれを1時間にすれば良いので、
$ 125KB \times 3600 = 450,000KB = 450MB $が最大転送可能量であることが分かりました。
後は最大転送可能量に対する転送データ量の割合を求めれば良いので、
$ \frac{220}{450} = 0.4888 \ldots $となり、約49%の【ウ】が正答となります。
問32【エ】
次のネットワークアドレスとサブネットマスクをもつネットワークがある。このネットワークを利用する場合,PCに割り振ってはいけないIPアドレスはどれか。
ネットワークアドレス:200.170.70.16
サブネットマスク :255.255.255.240
このようなサブネットマスクからホストアドレスを導き出すような問題で、割り振ってはいけないホストアドレスは「ネットワークアドレス」と「ブロードキャストアドレス」と「同一ネットワークでは無いアドレス」の3種類です。
ネットワークアドレス・・・ホストアドレスが全て「0」
ブロードキャストアドレス・・・ホストアドレスが全て「1」
つまり最終グループ(4つ目)を全て二進数に変換して、ホストアドレスを求めた後に、上記のどちらかに当てはまるかを判定すれば良いのです。
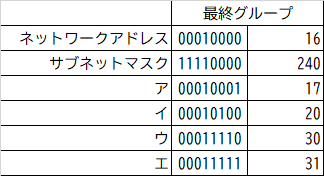
まず、どのアドレスもサブネットマスクによって出力されるアドレス(最終グループ前半4ビット)が一緒であることから、「同一ネットワークでは無いアドレス」は無いことが分かりました。
後はネットワークかブロードキャストアドレスのどちらかであるか判定すれば良いですが、エが明らかに後半4ビットに「1」が立っています。これはブロードキャストアドレスなので割り振れません。
よって【エ】が答えとなります。
問34【イ】
図はNTPによる時刻合わせの基本的な仕組みを表している。NTPサーバからの応答には,NTPサーバでの問合せ受信時刻と,応答送信時刻が含まれており,PCは図に示した四つの時刻からサーバ時刻とのずれを計算する。このとき,PCの内部時計はNTPサーバの時計と比べてどれだけずれているか。ここで,伝送遅延は問合せと応答で等しいものとする。また,図中の時刻は,PCとNTPサーバのそれぞれの内部時計の時刻であり,aa:bb:cc.dddddd は aa時bb分cc.dddddd秒 (ddddddはマイクロ秒)を表す。

PCの問い合わせから応答までにかかった時間を求めます。絶対値表記が好ましいので
$ 900-100=800 $としておきましょう。
次にNTPサーバーも同様に求めます。
$ 400-200=200 $となります。
ここから伝送遅延を求めると、$ 800-200=600 $ となります。
問題文には、伝送遅延は問合せと応答で等しいとあるので、
$ 600 \div 2 = 300 $ となります。
ここで、ずれが無ければ応答送信速度+伝送遅延=応答受信時刻となるはずです。
しかし実際に計算すると、 $400 + 300 = 700 \neq 900 $ となり計算が合いません。
つまり、この900と700の差がずれなのです。よって、
$ 900 – 700 = 200 $ となり、200ミリ秒の【イ】が答えとなります。
問48【エ】
まず、条件式を $ A or B $ といったように分けましょう。
複数条件網羅とはテストパターンが複数個ある条件の全てを網羅することです。
つまり、条件式$ A or B $のそれぞれ条件A、条件Bの真偽を「1」と「0」で全パターン表現すると、
$ ( A or B ) = ( 1 or 1 ), ( 1 or 0 ), ( 0 or 1 ), ( 0 or 0 ) $
となります。今回は真を1、偽を0として進めていきます。
問題文によって既に用意されているテストデータは、$ (A=4 , B=1) , (A=5 , B=0 ) $であるから、上記のパターンで言う、$ ( 0 or 0 ) , ( 0 or 1 ) $の二つである。
つまり、後 $ ( 1 or 1 ) , ( 1 or 0 ) $の二つを満たすような条件をテストデータとして用意すれば良い。
よって、残りの二つを満たすようなテストデータは【エ】しかあり得ない。

